Аннотация

      В статье предложен новый взгляд на динамику берегового прилива. Высказано предположение о преобразовании в береговой зоне части гидростатического напора Ньютонова приливного горба в гидродинамический напор. Показан механизм этого преобразования. Показано каким образом гидростатический напор величиной до 60 см. в открытом океане вызывает гидродинамический напор на берегу до нескольких метров.

 

     “У берегов океанов и морей дважды в сутки наблюдается поднятие (прилив) морской воды до некоторого максимального уровня (полная вода). После этого начинается опускание её (отлив) до минимального уровня (малая вода). Разность уровней большой и малой воды называется амплитудой прилива. Время между следующими друг за другом положениями полной (или малой) воды составляет 12 час. 25 мин. Это время точно совпадает с половиной промежутка времени, в течение которого Луна в своём видимом движении совершает полный оборот вокруг Земли”. [1]. И хотя причину приливов и отливов уже давно связывали с положением Луны на небесном своде, явление приливов представлялось человеку мистическим. Научное понимание природы приливов первым дал великий Ньютон исходя из своего закона всемирного тяготения. Следующий шаг был сделан Лапласом. С тех пор вплоть до наших дней предпринималось множество попыток объяснения всех практически наблюдаемых деталей явления. Однако “Полная теория приливов, отвечающая всем требованиям практики, ещё не создана”. [1]. Предложим наше видение явления берегового прилива, опираясь на статическую теорию Ньютона.

 

 

1. Теории приливов Ньютона и Лапласа

 

      Ньютон объяснил приливы неоднородностью поля тяготения Луны, что приводит к формированию двух статических поднятий поверхности океана (горбов) на линии, соединяющей центры Земли и Луны. Центры горбов всё время обращены к Луне и от неё как изображено на рисунке - 1. Рисунок взят из интернет-поисковика. Вследствие вращения Земли горбы бегут по поверхности океана, непрерывно следуя за движением Луны. По этой причине два последовательных прилива (или отлива) отделены друг от друга промежутком времени в 12 час. 25 мин., а скорость перемещения вершины горба по поверхности океана составляет порядка 1600 км/час.

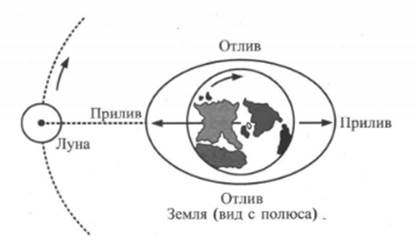
Рис. 1

 

      Однако статическая теория Ньютона столкнулась с противоречием наблюдаемых фактов. Согласно Ньютону полная вода на берегу должна наблюдаться в моменты времени, когда Луна находится по отношению к точке берега в зените (или наоборот), а малая вода - когда она находится в квадратуре. Как на рисунке - 1. В реальности между кульминацией Луны и последующей полной водой проходит значительный промежуток времени, составляющий несколько часов. Теория Ньютона не могла объяснить и того, что в одних районах бывает два береговых прилива в сутки, а в других только один, не объясняла  природу приливов на восточных берегах океанов и морей.

     Для снятия этих противоречий Лапласом была предложена динамическая теория приливов. В динамической теории приливы рассматриваются как волновое движение частиц воды в вертикальном и горизонтальном направлениях. Такой подход ставит под сомнение основное положение статической теории, о равновесии поверхности океана в каждый момент времени, которое не согласуется с достаточно быстрой сменой приливных явлений. Согласно теории Лапласа, массы воды, обладая значительной инерцией, не могут приходить мгновенно в равновесие при изменении действующих сил. Поэтому под действием непрерывно меняющейся периодической приливообразующей силы частицы воды, стремящейся к всё новым и новым положениям равновесия, получают стремление перейти их (вследствие инерции водных масс) и в последующем совершать колебания около положения равновесия. Так как приливообразующие силы действуют непрерывно с определённым периодом, то колебания поверхности океана незатухающие и характеризуются периодичностью вынуждающей силы. Динамическая волновая теория приливов относится к наиболее признанной, но и она не объясняет всей совокупности наблюдаемых эффектов приливных явлений. Она скорее только запутала и без того сложную ситуацию.

 

 

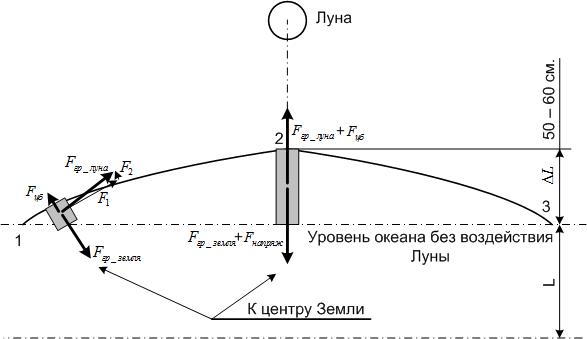
Рис. 2

 

Но главным видится не правомерность самого использования волновой теории для объяснения приливов. Массы воды в приливном горбе Ньютона не испытывают действие сил инерции. Силы инерции возникают при ускоренном движении массы под воздействием силы. В приливном горбе Ньютона силы, действующие на массы воды независимо от времени и географической точки, всегда уравновешены. Их результирующая на поверхности океана равна нулю. .

Для обоснования сказанного рассмотрим Рис. 2. На рисунке изображён приливный Ньютонов горб над простором океана. Серыми прямоугольниками обозначено поднятие уровня океана под воздействием притяжения Луны. На столб воды в приливном горбе действуют сила притяжения к центру Земли , центробежная сила, связанная с вращением Земли и направленная от центра Земли , сила притяжения Луны  и сила внутреннего напряжения , направленная против растяжения (сжатия). Сила притяжения Земли и центробежная сила постоянны и их суммарное действие обеспечивает уровень поверхности океана в случае отсутствия воздействия Луны. Это примерно уровень малой воды. Сила притяжения Луны переменна и меняется от нуля в квадратуре до максимума в горбах в данный момент времени, при этом горбы перемещаются по поверхности океана со скоростью примерно 1600 км/час. Под действием притяжения Луны верхний слой океана толщиной L растягивается на величину пропорциональную силе притяжения Луны в данной географической точке. Растяжение происходит до тех пор пока силы внутреннего напряжения, вызванные растяжением не сравняются с силой притяжения Луны. В точках 1 и 3 (в квадратуре) растяжение слоя L равно нулю, а в точке 2 на линии соединяющей центры Земли и Луны растяжение максимально. Это вершина горба. Вращение Земли происходит от точки 1 к точке 3 через точку 2. Отсюда горб перемещается от точки 2 в точку 1 за 6 час. 12,5 мин. При этом вода в горбе не переносится по поверхности океана с востока на запад. По мере перемещения горба, всегда ориентированного на Луну, по поверхности океана, слой L в точке 1 растягивается за 6 час. 12,5 мин. от нуля до максимума в 50 - 60 см. В точке 2 напротив за это время снижается от максимума до нуля. То есть в данной географической точке слой воды L сначала растягивается на  со скоростью примерно 10 см/час, а затем с той же скоростью опускается на уровень малой воды. При этом слой постоянно находится под нулевым силовым воздействием. Сила растяжения Луны всегда уравновешена силой внутреннего напряжения в слое. Следовательно силы инерции водных масс при растяжении и восстановлении первоначального уровня L не возникают и волновая теория в данной физической ситуации не применима. Ньютон прав. Теперь рассмотрим два столба жидкости в горбе растяжения, в положении 2, когда растяжение максимально и в положении 1 и 3, когда растяжение стремится к нулю на краях горба из-за соответствующего направления вектора сил притяжения Луны. Положение 2 это вершина горба. Возникает вопрос почему вода, обладая большой текучестью, не стекает с горба против градиента высот? Для этого рассмотрим слой вблизи точки 1. В точке 3 ситуация имеет зеркальное отображение. В точке 1 сила притяжения Луны по абсолютной величине практически та же, что и в точке 2, но её направление по отношению к направлению силы притяжения Земли сильно изменилось. Разложим силу притяжения Луны на две составляющие. Составляющая  направлена по линии к центру Земли. Её величина незначительна, отсюда растяжение слоя L стремится к нулю при приближении к точке 1. Составляющая  перпендикулярная  имеет большую величину и стремится к при приближении к токе 1. Но сила направлена в сторону горба и уравновешивается обратной ей силой внутреннего напряжения сжатия. Такая сила возникает в каждом столбе за исключением столба на вершине горба. Совокупность сил сжатия в сторону горба и удерживает горб от растекания. Таким образом мы обосновали как нам представляется правоту Ньютона о статичности приливного горба над просторами океана. Но в вновь возникают вопросы. Если под действием приливных сил Луны и Солнца массы воды над поверхностью океана статичны в точке координат, совершают только вертикальные движения и не переносятся по горизонтали с востока на запад, то на берегу во время прилива наблюдается массовый перенос по горизонтали. Явление носит очевидный гидродинамический характер. При этом, что замечательно, статический горб имея высоту порядка 50 - 60 см. вызывает подъём воды на берегу над уровнем перед приливом до нескольких метров. Возникает вопрос об энергиях и силах приводящих к этому эффекту. Если над океаном приливная сила всегда направлена на центр Луны и центр Солнца (векторная сумма), то у береговой линии возникает сила параллельная поверхности воды и направленная на берег? А статический напор в 50 - 60 см. на береговом склоне создаёт гидродинамический напор в несколько метров? Остаются открытыми вопросы об одном и двух суточных приливах и о приливе на восточном берегу океана. Попытаемся ответить на эти вопросы в следующем разделе.

 

 

2. Береговой прилив

 

     К западному, условно меридиональному берегу океана приливный Ньютонов горб, с накопленной потенциальной энергией, движется с относительной скоростью 1600 км/час. При этом его величина на приливном “экваторе” в данной точке берега изменяется за  6 час. 12,5 мин. по высоте от нуля до 50 - 60 см. Соответственно меняется и потенциальная энергия горба в данной точке берега. По меридиану эта высота на север и юг снижается до нуля в точках квадратуры. Рассмотрим события и явления в данной точке береговой линии за этот период. Начнём рассмотрение с момента, когда приливный горб только коснулся берега и уровень воды соответствует малой воде. Как на рисунке - 3. Рассмотрим два варианта берегового склона. В первом варианте (верхняя часть рисунка) берег имеет вертикальный обрыв. При этом глубина обрыва значительно превосходит толщину слоя L, подвергающегося растяжению под действием сил притяжения Луны.

    

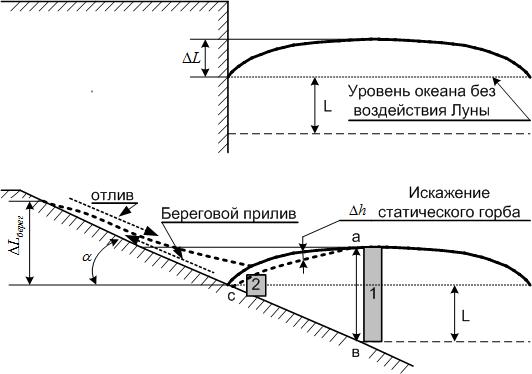
Рис. 3

 

      Величина (толщина) растягивающего слоя L видимо не более чем на порядок выше высоты горба (50 -  60 см.), во всяком случае вряд ли более чем на два порядка, учитывая что величина притяжения вод океана к центру Земли многократно больше притяжения к Луне. Величину L достаточно просто можно определить экспериментально. Это та минимальная глубина вертикального обрывистого берега, на которой максимум берегового прилива совпадает по времени с моментом прохождения пика горба (момент кульминации Луны в данной точке) над этим обрывистым берегом. Сейчас мы это попытаемся объяснить.  Когда Луна и соответственно приливный горб приближаются к берегу, то усиливается притяжение Луны и соответственно происходит растяжение столба воды у береговой линии (у обрыва). Начинается прилив. Когда кульминация Луны совпадает с точкой обрыва растяжение столба достигает максимума (50 -  60 см.). Это момент полной воды. Затем, когда после прохождения максимума, высота горба за следующие 6 час. 12,5 мин. снижается с максимума до нуля, происходит отлив. Таким образом у обрывистого западного берега океана теория прилива Ньютона полностью соответствует наблюдаемым фактам. Полная вода соответствует моменту кульминации Луны над данной точкой, происходит два прилива за сутки.

      Теперь рассмотрим события и явления на береговом склоне имеющем угол  к уровню океана (нижняя часть рисунка - 3). Здесь ситуация меняется в сравнении с обрывистым берегом. И связано это с тем, что слой воды L, подвергающийся растяжению, сокращается при приближении к точке с (уровень малой воды) до нуля с максимального значения на линии а - в, касания слоя L берегового склона. К чему это приведёт? Слой L в точке касания берегового склона (точка в) растянут под действием притяжения Луны полностью и, как мы выяснили в предыдущем разделе, находится в статическом равновесии. Сумма всех сил действующих на слой равна нулю. Его высота соответствует статическому приливному горбу в данной географической точке. Как  и  всех  столбов  расположенных  правее  линии  а - в.  А вот любой столб слоя L, находящийся левее линии а - в, имея меньшую высоту растяжения из-за пологого склона, уже не может растянуться до высоты соответствующей статическому состоянию приливного горба. Это приводит на береговом склоне (линия в - с) к искажению уровня статического горба на некоторую величину , что нарушает равновесие сил в полосе в - с. Более правый столб воды имеет не скомпенсированную высоту по отношению к левому. Возникает не скомпенсированный градиент высоты приливного горба, порождающей силу направленную на берег. Эта сила и преобразует не скомпенсированный градиент потенциальной энергии в гидродинамический напор воды по причине её высокой текучести. Не скомпенсированный статический напор  имеет незначительную величину в сравнении с максимумом статического напора горба. Но он действует в полосе в - с в течении 6 час. 12,5 мин., передовая этому слою воды всё новые порции энергии, от надвигающегося Ньютонова приливного горба. Действует своеобразный насос. Вода устремляется по береговому склону вверх, достигая максимальной высоты в момент, когда переданная гидродинамическая энергия полностью преобразуется в статический напор на берегу и частично растратится на трение. Наступит максимум берегового прилива, полная вода. С этого момента под действием статического напора на берегу начинается отлив. Но так как скорость гидродинамического потока берегового прилива не сопоставимо меньше скорости перемещения вершины статического приливного горба (1600 км/час) и происходит запаздывание полной воды по отношению к моменту кульминации Луны. Причём чем круче береговой склон (больше угол) тем меньше запаздывание. При этом при крутом склоне, несмотря на запаздывание происходит два береговых прилива. Напротив при некотором малом угле  возникает ситуация, что за 6 час. 12,5 мин. гидродинамический напор не успевает преобразоваться в статический напор на берегу и поток получает новую порцию энергии от второго приливного горба. Это формирует суточный прилив. Вода на берегу поднимается на практически вдвое большую величину и затем более мощный отлив преодолевает промежуточное воздействие последующего полусуточного горба. В этом физика суточного прилива.

     Теперь остановимся на береговом приливе восточного берега океана, который вроде бы противоречит теории приливов Ньютона. Но это не так. Ситуация возникновения гидродинамического напора та же, что и на западном берегу океана, но имеет зеркальное отображение. Здесь накачка энергии в береговой прилив начинается в момент кульминации Луны над береговой точкой и заканчивается через 6 час. 12,5 мин. 

     Характеристики берегового прилива в данной местности зависят от многих причин и параметров. Это фазы Луны и Солнца, их склонение, очертания берега, характер рельефа дна, наличие островов, трение, морские течения и ветры, деформация земного шара под действием приливообразующих сил и множество других трудно учитываемых фактов. Тем не менее накопленный наблюдательный материал по интересующим береговым линиям, их анализ и систематизация, позволяет решать все практические задачи. Данная работа представляет скорее чисто академический интерес и позволяет в принципе объяснить всю совокупность наблюдаемых приливных эффектов.

 

Заключение

     Теория приливного горба предложенная Ньютоном справедлива для открытых просторов океана. В массе воды приливного горба накапливается потенциальная энергия гравитационного взаимодействия Луны и океана, при этом локальный объём воды в приливном горбе испытывает нулевое суммарное силовое воздействие в каждый момент времени. Здесь действует гидростатика. Относительное перемещение приливного горба над просторами океана по причине суточного вращения, не сопровождается переносом масс воды. При приближении к береговой линии равновесие сил, приложенных к локальному объёму воды в приливном горбе нарушается. Возникает не скомпенсированный градиент потенциальной энергии, который и вызывает массовое движение на берег в соответствии с законами гидродинамики.

 

Литература

1. Сивухин Д.В. Общий курс физики. – М: “Наука”, 1979г. Том 1, 519с.

2. Хазиров Юсуп. Приливы и отливы - результат вращения Земли и водоворотов.

3 Шулейкин В.В. Физика моря. – М: “Наука”, 1968г., 1090с.

4. Щевьев В.А. Приливообразующие силы Луны и Солнца - причина образования длиннопериодных волновых течений в океане.

 

P.S. Доклад представлен на 21-й Межвузовской Российской научной конференции “Векторная энергетика в технических, биологических и социальных системах”. Балаково, март, 2019г.