


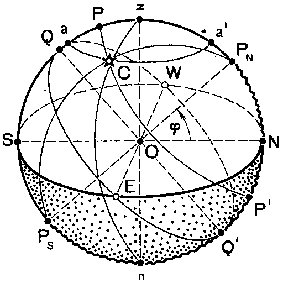
Горизонтная система координат
Азимут светила А — сферический угол при зените или дуга
истинного горизонта между меридианом наблюдателя и вертикалом светила.
Применяются три системы счета азимута. При полукруговом
(практическом) счете за точку начала отсчета в северном полушарии принимают
точку N, а в южном — точку S, т. е. точка начала отсчета полукругового азимута
всегда одноименна с наименованием широты места наблюдателя. Азимуты
ограничиваются пределом в 180°. При четвертном счете азимуты отсчитываются от
точек N и S в сторону Е и W от 0 до 90°. При круговом (навигационном) счете
азимут отсчитывается в любой широте от точки N в сторону Е от 0 до 360°.
Высота светила h — угол при центре небесной сферы или
дуга круга высоты (вертикала) между истинным горизонтом и центром светила.
Высота отсчитывается от 0 до + 90° к зениту и от 0 до — 90° к надиру.
Отрицательная высота называется снижением светила.
Дополнение высоты до
90°, т. е. дуга между зенитом и светилом, называется зенитным
расстоянием z. Зенитное расстояние отсчитывается от зенита и
изменяется от 0 до 180°.
Если светило находится на
меридиане наблюдателя, то его высоту называют меридиональной высотой H, а
зенитное расстояние — меридиональным зенитным расстоянием Z.
z+ h = 90°;
Z + Н = 90°;
z = 90° - h;
Z = 90° - H.
Первая система экваториальных координат
Часовой угол светила t —
сферический угол при полюсе мира или дуга экватора между меридианами наблюдателя и светила.
Вторая система экваториальных координат
Одной координатой в этой системе является, как и в первой,
склонение светила d, а в другой —
прямое восхождение
a —
сферический угол при полюсе мира. а измеряется дугой небесного экватора от точки
весеннего равноденствия (точка Овна g) в сторону, обратную
вращению небесной сферы, до меридиана светила, т. е. в сторону движения Солнца
по эклиптике.
Точка Овна находится на пересечении
эклиптики с небесным экватором. В этой точке Солнце находится ежегодно 21
марта.
Эклиптика — плоскость, в которой движется Земля
вокруг Солнца или большой круг небесной сферы (наклоненный к небесному экватору
под углом 23°27"), по которому перемещается центр Солнца в его видимом годовом
движении, отражающем движение Земли по ее орбите.
Величина, дополняющая прямое восхождение до 360°, называется
звездным
дополнением t*,
Экваториальные координаты светил можно выбрать на любой момент из Морского Астрономического Ежегодника (МАЕ).
Параллактический треугольник
и преобразование сферических координат
Сферический треугольник на небесной сфере, образованный пересечением меридиана наблюдателя, вертикала и меридиана светила, называется параллактическим, или полярным, треугольником светила. В зависимости от наименования широты места наблюдателя за постоянную вершину треугольника принимают повышенный Северный или Южный полюс мира (см. рисунок).
Основные соотношения между элементами параллактического треугольника
| Величины | Расчетная формула | Определяемая величина и ее применение | |
| данные | иском. | ||
| φ, d, t | h | sin h = sin φ sin d + cos φ cos d cos t | Счислимая высота в способе высотных линий |
| φ, d, t | A | ctg A = cos φ tgd cosec t — sin φ ctg t | Поправка компаса для нахождения ИП светила |
| φ, d, A | t | Из предыдущей формулы при А = 90° cos t = ctg φ + tg d | Часовой угол светила, находящегося на первом вертикале |
| φ, d, h | t | cos t = sec φ sec d sin h — tg φ+ tg d | Местный часовой угол |
| φ, d, h | t |
Из предыдущей формулы при h = 0 cos t = tg φ + tg d |
Время истинного восхода и захода светил |
| φ, d, A | d | sin d = sin φ sin h + cos φ *cos h cosA | Склонение светила |
| h, φ | A |
Из предыдущей формулы при h =
0 cos A = sin d sec φ |
Азимут восхода или захода светил |
| А, φ | h |
Из той же формулы при А= 90° sin h = sin d cosec φ |
Высота светила на первом вертикале |
| h,d, q | φ |
sin φ = sin h sin d + cos h cos d cos q |
Широта места судна |
| h,d, t |
А |
sin A = cos d sin t sec h |
Азимут в способе высотных линий и при определении поправки компаса по Полярной звезде |
Определение знаков и значений координат
| Координаты | Знаки координат и их значения | Знаки тригонометрических функции |
|
Широта j(N или S) |
Всегда (+)
Меньше 90° |
Все функции (+) |
|
Одноименно с j (+) |
Все функции (+) | |
|
Склонение d(N или S) |
Разноименно с
j (в IV четверти) (-) |
cos и sec (+), остальные (—) |
| Меньше 90° | ||
| Высота h |
Над горизонтом (+) |
Все функции (+) |
|
Под горизонтом |
cos и sec (+), остальные (—) | |
| Меньше 90° | ||
|
Азимут А |
Меньше 90° (в 1 четверти) | Все функции (+) |
|
Больше 90° (во 11 четверти) |
sin и cosec
(+), | |
|
Если правая часть формулы с минусом, то А больше 90°. Первая буква наименования по j, вторая — по t | ||
|
Часовой угол t (практический) |
Меньше 90° (в I четверти) |
Все функции (+) |
|
Больше 90° (во II четверти) |
sin и
cosec (+), | |
| Если правая часть формулы с минусом, то t больше 90°. Наименования по второй букве азимута или по указаниям к таблицам, применяемым при вычислениях |
Наименование азимута четвертого счета при вычислении по sin A
| Наименование d | Значение |
1-я буква азимута |
2-я буква азимута | |
|
d |
hс | |||
| Разноименно с широтой |
Не имеют значения |
Разноименна с широтой |
Всегда одного наименования с часовым углом (практическим) | |
| Одноименно с широтой | d < j |
hс > h1 |
То же | |
| То же | d < j | hс < h1 | Одноименна с широтой | |
|
То же |
d > j | Не имеет значения | То же | |
Примечание:
h1 — высота светила на первом вертикале по данным табл. 21 Мореходных таблиц МТ—75.
Координаты Солнца
Экваториальные координаты Солнца
| День | Дата |
Склонение dÅ, град |
Прямое восхождение aÅ ,град. |
| Весеннего равноденствия | 21.03 | 0 | 0 |
| Летнего солнцестояния | 22.06 | 23,5N | 90 |
| Осеннего равноденствия | 23.09 | 0 | 180 |
| Зимнего солнцестояния | 22.12 | 23,5S | 270 |
Суточное изменение склонения Солнца
dÅ в течение месяца
до и после дней весеннего и осеннего равноденствия равно 0,4°, в течение месяца
до и после дней летнего и зимнего солнцестояний — 0,1°, в течение второго месяца
после дней 21.03, 22.06, 23.09, и 22.12—0,3°.
Суточное
изменение прямого восхождения Солнца
aÅ
в течение всего года 1°.
Точные значения координат на любой момент выбирают из Морского астрономического
ежегодника (МАЕ).
С помощью приведенных данных можно найти
приближенную меридиональную высоту HÅ
Солнца на данную
дату в широте судна. Для этого рассчитываем на заданную дату
dÅ, затем
находим
Z
Å @ j — dÅ и HÅ = 90° — ZÅ.Например, 25 декабря
dÅ = 23,2° S. В широте (j = 45,5° N; ZÅ = 45,5° — (— 23,2°) = 68,7°; HÅ = 21,3°.Как найти основные звезды - смотрите по этой ссылке слева.
Астрономические наблюдения - смотрите по этой ссылке.